岩波データサイエンスvol.3のCM接触の因果効果を他の方法で推定してみた(2)

岩波データサイエンスvol.3
Causal Forest
Causal Forest による因果効果の推定
おわりに
統計的因果推論の関連記事

岩波データサイエンスvol.3

岩波データサイエンスvol.3のCM接触の因果効果を他の方法で推定してみた、第二弾です。今回は「非均質性を伴った処置効果(Heterogeneous Treatment Effects)」の推定で数年前に提唱された Causal Forest を用いてみたいと思います。なお、岩波データサイエンスvol.3のCM接触の因果効果を他の方法で推定してみた(1) - YuRAN-HIKOでも傾向スコアマッチングを用いた記事があります。ご興味のある方は併せてお読みください。

使用するデータや用いる説明変数に関しては前回の記事と同様になります。では、早速分析を進めていきたいと思います。今回も R言語を用いることとします。

Causal Forest

Causal Forest とは 2015年に S. Wager と S. Athey によって提唱された、ランダムフォレストを用いた「非均質性を伴った処置効果(Heterogeneous Treatment Effects)」の推定手法です*1。日本語でも他の方が分かりやすい説明をしてくださっているのでここでの繰り返しは控えますが、暴言であるのを承知の上であえて簡単に述べるとするならば「最終的に推定したい変数 Y ではなく、割り当て変数 W を目的変数とした Propensity Tree を Forest にしたもの = Causal Forest」という理解をしています*2。

特に目を引くのが処置の「平均的な効果」ではなく、1つ1つの観察対象によって異なる「非均質性を伴った処置効果」の推定を行うことができる点かと思います。この推定精度が上がることによって、例えば薬Aの処置効果が平均して○○という形ではなく、aさんに対する薬Aの処置効果は△△、bさんに対する効果は□□......といったようなことができると期待されており、左記のような医学 / 薬学のドメインだけでなく、因果効果の非均質性が問題になる社会科学系の諸分野やビジネス領域でも期待されているのではないかと勝手に思っています。

Causal Forest による因果効果の推定

では早速『岩波データサイエンスvol.3』中のCM接触の因果効果推定で用いられたデータに対して、Causal Forest を使って因果効果の推定を行ってみようと思います。データの取得部分は前回の記事とまったく同じです。前回と異なり、今回は因果効果の推定のためにデータを Train / Test に分割しています。分割比率は雑ですが、データが全件で 10,000 あるため、いったん 20%としておきます。

# データのダウンロード
> library(devtools)
> filepath <- "https://raw.githubusercontent.com/iwanami-datascience/vol3/master/kato%26hoshino/q_data_x.csv"
> df <- read.csv(url(filepath))

# Train / Test にデータを分割
> set.seed(1234)
> test_pos <- sample_frac(df[df$cm_dummy==1,], 0.2)
> test_neg <- sample_frac(df[df$cm_dummy==0,], 0.2)
> df_test <- rbind(test_pos, test_neg)
> df_train <- anti_join(df, df_test)

　
次に、必要なライブラリのインポートを行います。Causal Forest を含む、ランダムフォレストを活用した諸分析手法は grf というパッケージに内包されています。ちなみに、grf は「一般化ランダムフォレスト(Generalized Random Forest)」の略称です*3。ちなみに、この一般化ランダムフォレストも上述の S. Wager や S. Athey によって提唱されたアルゴリズムです*4。

Causal Foerst を適用する関数はその名の通り causal_forest になります。引数として共変量 X、因果効果を推定する最終的な目的変数 Y、割り当て変数 W を与える必要があるため、まずはそれらをベクトル化します。パラメータの設定はいったんデフォルトで、かつ乱数のシード値を固定しておくこととします。

# Train
> X <- df_train %>%
    dplyr::select(TVwatch_day, age, sex, 
                    marry_dummy, child_dummy, 
                    inc, pmoney, area_kanto,
                    area_tokai, area_keihanshin, 
                    job_dummy1, job_dummy2, 
                    job_dummy3, job_dummy4,
                    job_dummy5, job_dummy6, 
                    job_dummy7, fam_str_dummy1, 
                    fam_str_dummy2, fam_str_dummy3, 
                    fam_str_dummy4
                   )
> W <- df_train$cm_dummy
> Y <- df_train$gamesecond

> tau_forest <- causal_forest(X, Y, W, seed = 42)
> tau.forest

GRF forest object of type causal_forest 
Number of trees: 2000 
Number of training samples: 8000 
Variable importance: 
    1     2     3     4     5     6     7     8     9    10    11    12    13    14    15    16    17 
0.259 0.043 0.004 0.005 0.013 0.181 0.252 0.009 0.004 0.011 0.003 0.113 0.000 0.000 0.005 0.001 0.070 
   18    19    20    21 
0.022 0.001 0.006 0.001

　
変数の重要度を Variable importance で簡単に確認することができるので便利ですね。
次に、訓練データに対する処置効果をOOB(Out-of-Bag)によって推定します。今回は処置効果のヒストグラムの描画を行うにあたって、あえて階級数を多めに取っています。

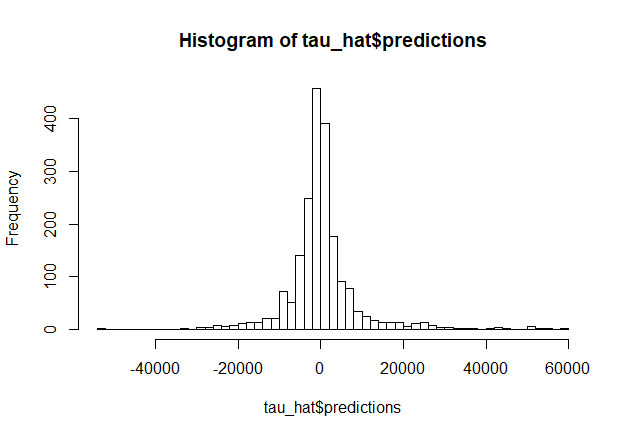
# OOB で Train データにおける効果を推定
> tau_hat_oob <- predict(tau_forest)
> hist(tau_hat_oob$predictions, breaks=50)

> mean(tau_hat_oob$predictions)
[1] 398.8847

> quantile(tau_hat_oob$predictions, probs = c(.05, .25, .5, .75, .95))
         5%         25%         50%         75%         95% 
-11161.4368  -2799.9774   -195.2798   2360.6314  14452.2143

次に、上記のモデルを Test データに適用し、因果効果の推定を行うこととします。コード部分は非常にシンプルです。

# Test
> X_test <- df_test %>%
    dplyr::select(TVwatch_day, age, sex, 
                    marry_dummy, child_dummy, 
                    inc, pmoney, area_kanto,
                    area_tokai, area_keihanshin, 
                    job_dummy1, job_dummy2, 
                    job_dummy3, job_dummy4,
                    job_dummy5, job_dummy6, 
                    job_dummy7, fam_str_dummy1, 
                    fam_str_dummy2, fam_str_dummy3, 
                    fam_str_dummy4
                   )

> tau_hat <- predict(tau_forest, X_test, estimate.variance=TRUE)
> hist(tau_hat$predictions, breaks=50)

> mean(tau_hat$predictions)
[1] 319.7155
> quantile(tau_hat$predictions, probs = c(.05, .25, .5, .75, .95))
         5%         25%         50%         75%         95% 
-10521.4485  -2912.6860   -244.0363   2283.4407  15130.7626

こうしてみると、平均的な処置効果としてはプラスなのですが、中央値がマイナスなため対象者の過半数はCM接触によって逆にゲームのプレイ時間が減る......といった推定になっています*5。今回のデータには含まれていないのでこれ以上の分析はできませんが、CM開始以前に当該のゲームを遊んだことがあるかを示す変数がデータに含まれていれば、CM開始以前のゲームの接触状況別にセグメントを切って効果を見ることもできるかもしれません。

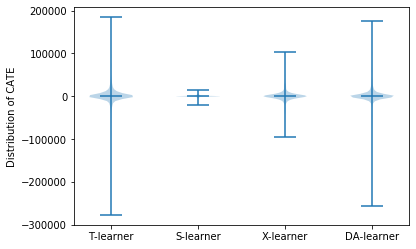
最後に、今回の結果による「条件付き平均処置効果(CATE = Conditional Average Treatment Effect)」の推定を行います。条件付き平均処置効果の推定にはいくつかの種類(CATE / CATT / CATC)があるのですが、今回のデータはどうやら割り当て変数の推定値のオーバーラップがあまりよくないため、傾向スコアによる重みづけを行った処置効果(target.sample = "overlap")を表示することにします。

> average_treatment_effect(tau.forest, target.sample = "overlap", method = "AIPW")
estimate  std.err 
200.7810 594.1308

おわりに

以上、『岩波データサイエンスvol.3』のCM接触の因果効果を Causal Forest を用いて推定してみました。おそらく自分の理解不足ゆえに間違っているところや不足している点も多いかと思いますが、そこはどうかやんわりとご教示いただけますと幸いです......。当然と言えば当然かもしれませんが、せっかく Heterogeneous に効果を推定した上で Average な処置効果をはじき出してもあんまり意味はなさそうで、どちらかというと Heterogeneous に効果を推定し、効果がプラスになる対象者にのみキャンペーンを打つとか、投下コストに対してリターンが十分に望める対象にだけターゲティングして施策を実施するといった際に使うのが良いのだろうなと感じています。このあたりはさらに勉強してうまく実社会の課題解決に繋げられるような活用法を見出せるようにならねば、といったところです。