岩波データサイエンスvol.3のCM接触の因果効果を他の方法で推定してみた(3)

はじめに
Meta-Learner
因果効果の推定
おわりに
統計的因果推論の関連記事

はじめに

岩波データサイエンスvol.3のCM接触の因果効果を他の方法で推定してみた、第三弾です。第一弾で「傾向スコアマッチング」と「Causal Forest」の2つを取り上げると書きましたが、自身の勉強もかねて追加でもう1本試してみることにしました。
第三弾は Causal Forest と並んで「非均質性を伴った処置効果(Heterogeneous Treatment Effects)」の推定法として近年注目を集めている Meta-Learner という手法を試してみたいと思ます。
なお、例によって傾向スコアマッチングを用いた前々回の記事、ならびに Causal Forest を用いた前回の記事は以下にありますので、ご興味のある方はこちらも併せてお読みください。

yuranhiko.hatenablog.com

使用するデータや用いる説明変数に関しては前々回、前回の記事と同様になります。今回は Meta-Learner の手法を試すにあたって 2018年に Microsoft Research が開発した EconML という Python ライブラリを用いることとします。

Meta-Learner

まずは分析を始める前に、Meta-Learner に関して簡単な紹介をしたいと思います。
Meta-Learner とは 2017年に S. Kunzel らによって提唱された因果推論の手法で、「条件付き平均処置効果 (CATE = Conditional Average Treatment Effects)」を推定するためのメタ・アルゴリズムのことを指します*1。2018年に Microsoft Research が開発した EconML ライブラリの中にこのアルゴリズムが実装されており、Meta-Learner は　Causal Forest と並んで機械学習を用いた「非均質性を伴った処置効果」の推定法として注目を集めています*2。
EconML ライブラリの中では Meta-Learner にカテゴライズされる複数の推定手法が含まれていますが、今回はそれらのうち T-Learner / S-Learner / X-Learner / Domain Adaptation Learner の4手法について試してみたいと思います*3。まずは、それぞれのアルゴリズムに関する超簡単な説明から始めます。

T-Learner

T-Learner は処置を行わなかった場合のアウトカム $Y(0)$ と処置を行った場合のアウトカム $Y(1)$ を別々に予測して因果効果を推定する手法です。CATE の推定値は以下で与えられます。

$\hat{\tau}(x) = E[Y(1) - Y(0) | X=x$ ]
$= E[Y(1) | X=x$ ] $- E[Y(0) | X=x$ ]
$= \hat{\mu_1}(x)$ $- \hat{\mu_0}(x)$

ただし $\hat{\mu_0}(x)= M_0(Y^{0} ～ X^{0})$ / $\hat{\mu_1}(x)= M_1(Y^{1} ～ X^{1})$ はそれぞれ対象群と処置群におけるアウトカムを指します。また $M_0$ と $M_1$ は特徴量とアウトカムの関係を学習する機械学習アルゴリズムであれば何でも適用可能です。

S-Learner

S-Learner は処置割り当て変数 $T$ を他の特徴量 $X$ とともにインプットとして与えた上で、 $Y(0)$ と $Y(1)$ を同一のモデルで学習します。CATE の推定値は以下で与えられます。

$\hat{\tau}(x) = E[Y | X=x, T=1] - [Y | X=x, T=0]$
$= \hat{\mu}(x, 1) - \hat{\mu}(x, 0)$

ただし $\hat{\mu} = M(Y ～ (X, T))$ は特徴量 $X$ と $T$ のアウトカムです。 $M$ は T-Learner の時と同様、特徴量からアウトカムの関係を学習する機械学習アルゴリズムであれば何でも適用可能です。

X-Learner

X-Learner は「処置群に対する条件付き平均処置効果(CATT = Conditional Average Treatment Effect on the Treated)」と「対照群に対する条件付き平均処置効果(CATC = Conditional Average Treatment Effect on the Controls)」を推定するために $Y(1)$ と $Y(0)$ を別々にモデル化し、CATE の推定には傾向スコアで重みづけした CATT と CATC を用いています。

$\hat{\mu_0} = M_1(Y^{0}∼X^{0})$
$\hat{\mu_1} = M_2(Y^{1}∼X^{1})$
$\hat{D^{1}} = Y^{1} - \hat{\mu_0}(X^{1})$
$\hat{D^{0}} = \hat{\mu_1}(X^{0}) - Y^{0}$
$\hat{\tau_0} = M_3(\hat{D^{0}} ～ X^{0})$
$\hat{\tau_1} = M_4(\hat{D^{1}} ～ X^{1})$ $\hat{\tau} = g(x)\hat{\tau_0}(x) + (1 - g(x))\hat{\tau_1}(x)$

ただし $g(x)$ は $P[T=1|X]$ の推定値です。 $M_1$ / $M_2$ / $M_3$ / $M_4$ は特徴量からアウトカムの関係を学習する機械学習アルゴリズムを指します。

Domain Adaptation Learner

Domain Adaptation Learner とは X-Learner の派生形で、 $P(X^{0})$ と $P(X^{1})$ の確率分布が異なることが想定される場合に用いられます。 $X^{0}$ のサンプルを用いて訓練を行う際、それが $X^{1}$ のサンプルにどれだけ近しいかで重みづけを行います。

$\hat{\mu_0} = M_1(Y^{0}∼X^{0}, weights= \displaystyle \frac{g(X^{0})}{(1−g(X^{0}))})$
$\hat{\mu_1} = M_2(Y^{1}∼X^{1}, weights= \displaystyle \frac{(1−g(X^{1}))}{g(X^{1})})$
$\hat{D^{1}} = Y^{1} - \hat{\mu_0}(X^{1})$
$\hat{D^{0}} = \hat{\mu_1}(X^{0}) - Y^{0}$
$\hat{\tau} = M_3(\hat{D^{0}} | \hat{D^{1}} ～ X^{0} | X^{1})$

ただし $g(x)$ は $P[T=1|X]$ の推定値です。 $M_1$ / $M_2$ / $M_3$ は特徴量からアウトカムの関係を学習する機械学習アルゴリズムを指し、 $|$ はデータセットの接続を指します。

因果効果の推定

お待たせしました。それでは『岩波データサイエンスvol.3』中のCM接触の因果効果推定で用いられたデータに対して、Meta-Learner の上記4つの手法を使って因果効果の推定を行ってみようと思います。
データの取得部分は前回の記事とまったく同じです。Train / Test の分割比率もいったん 20%とし、割り当て変数(cm_dummy)の値で層化分割を行います。また、今回はいったん試験的にアルゴリズムを試してみることを目的とし、アウトカムの予測モデルには勾配ブースティングを、傾向スコアのモデルにはランダムフォレストを用いることとします。また、パラメータ調整も最小限とします。
まずはライブラリのインポートから。econml.metalearners が各種 Meta-Learner を実装するためのライブラリです。

#ライブラリのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

from econml.metalearners import TLearner, SLearner, XLearner, DomainAdaptationLearner
from sklearn.ensemble import RandomForestClassifier, GradientBoostingRegressor
from sklearn.model_selection import train_test_split

　
次にデータのダウンロードと前処理を行います。このあたりは特筆するところはなく、いつも通りデータのダウンロードと特徴量の選定を行います。

# データのダウンロード
filepath = "https://raw.githubusercontent.com/iwanami-datascience/vol3/master/kato%26hoshino/q_data_x.csv"
df = pd.read_csv(filepath)

## 特徴量 X、アウトカム Y、割り当て変数 W
X = df[['area_kanto', 'area_tokai', 'area_keihanshin', 'age', 'sex', 'marry_dummy', 
        'job_dummy1', 'job_dummy2', 'job_dummy3', 'job_dummy4', 'job_dummy5', 
        'job_dummy6', 'job_dummy7', 'inc', 'pmoney', 'fam_str_dummy1', 'fam_str_dummy2', 
        'fam_str_dummy3', 'fam_str_dummy4', 'child_dummy', 'TVwatch_day']]
Y = df['gamesecond']
W = df['cm_dummy']

# データを訓練データとテストデータに分割。割り当て変数 W で層化
X_train, X_test, Y_train, Y_test, W_train, W_test = train_test_split(X, Y, W, test_size=0.2, shuffle=True, random_state=42, stratify=W)

　
ここから実際に Meta-Learner を用いたモデリングを行っていきます。Meta-Learner は scikit-learn ライクかつシンプルで非常に使いやすい形になっており、学習用の機械学習モデルを引数にとってインスタンスを作成した後、.fit で訓練を、.effect で CATE の推定を行うことができます。まずは T-Learner による推定から行っていきます。

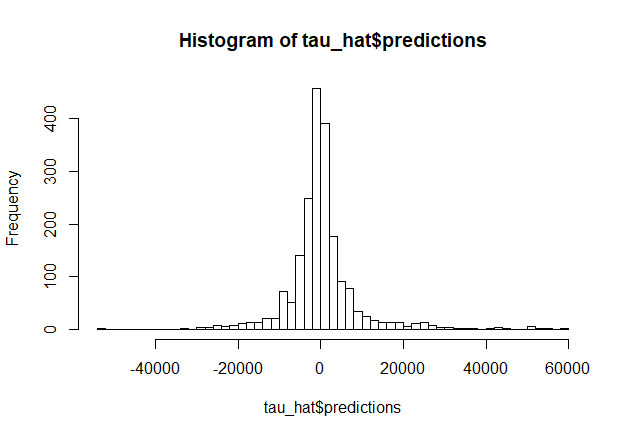
n = len(X_test)

#T-Learner のインスタンス作成
models = GradientBoostingRegressor(n_estimators=100, max_depth=6, min_samples_leaf=int(n/100), random_state=42)
T_learner = TLearner(models)

#T-Learner の訓練
T_learner.fit(Y_train, W_train, X_train)

#テストデータでCATEを推定
T_te = T_learner.effect(X_test)

#CATEの推定結果を確認
print("CATE of T-learner: ", round(np.mean(T_te), 2))
> CATE of T-learner:  1093.02

print("Percentile of CATE of T-learner: ", np.quantile(a=T_te, q=[.05, .25, .5, .75, .95]))
> Percentile of CATE of T-learner:  [-17206.88  -2771.39    501.09   5016.37  22522.09]

　
T-Learner による CATE 推定値の平均は 1,093となりました。もう少しちゃんと推定を行うにあたっては使用する機械学習のモデルを XGBoost や LightGBM にしてみたり、cross validation + ハイパラチューニングを行った方がよさそうな気がしますが、上記のコードのみで簡単に因果効果を推定できてしまうのは素晴らしいですね。

ついで、S-Learner / X-Learner / Domain Adaptation Learner による CATE の推定を行います。それぞれアルゴリズムの差に起因する多少の違いはあれ、要領は T-Learner と大きくは変わりません。

#S-Learner のインスタンス作成
overall_models = GradientBoostingRegressor(n_estimators=100, max_depth=6, min_samples_leaf=int(n/100), random_state=42)
S_learner = SLearner(overall_models)

#S-Learner の訓練
S_learner.fit(Y_train, W_train, X_train)

#テストデータでCATEを推定
S_te = S_learner.effect(X_test)

#CATEの推定結果を確認
print("CATE of S-learner: ", round(np.mean(S_te), 2))
> CATE of S-learner:  337.55

print("Percentile of CATE of S-learner: ", np.quantile(a=S_te, q=[.05, .25, .5, .75, .95]))
> Percentile of CATE of S-learner:  [-2664.26  -162.66    77.77   565.23  3833.35]

　
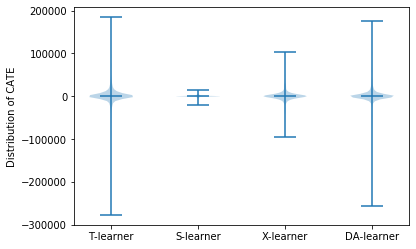
S-Learner の推定結果は T-Learner と比べてかなりばらつきが小さく、平均値も控えめになりました。このばらつきは実際の処置効果と推定値との差分のばらつきではなく、あくまで各ユーザーに対する処置効果の推定値のばらつきである点に注意してください。 Kunzel et al.(2019) にもありますが、S-Learner は割り当て変数 W で木の分割を行わないケースがままあり、処置効果の推定がゼロに寄りやすいバイアスがあるとのことなので、そのあたりがこの結果の背景にあるのかもしれません*4。

#X-Learner のインスタンス作成
models = GradientBoostingRegressor(n_estimators=100, max_depth=6, min_samples_leaf=int(n/100), random_state=42)
propensity_model = RandomForestClassifier(n_estimators=100, max_depth=6, min_samples_leaf=int(n/100), class_weight='balanced_subsample', random_state=42)
X_learner = XLearner(models=models, propensity_model=propensity_model)

#X-Learner の訓練
X_learner.fit(Y_train, W_train, X_train)

#テストデータでCATEを推定
X_te = X_learner.effect(X_test)

#CATEの推定結果を確認
print("CATE of X-learner: ", round(np.mean(X_te), 2))
> CATE of X-learner:  786.63

print("Percentile of CATE of X-learner: ", np.quantile(a=X_te, q=[.05, .25, .5, .75, .95]))
> Percentile of CATE of X-learner:  [-13941.23  -2892.24    351.55   3635.49  19824.67]

　
X-Learner は T-Learner や S-Learner と異なり、傾向スコアを推定するモデルも引数に加える必要があります。実行結果としてはは今回のケースでは比較的 T-Learner に近めで、T-Learner よりもやや控えめな推定結果となりました。Kunzel et al. (2019) では CATE が複雑な場合、すなわち処置群 / 対照群の双方において、もう片方の群から学習する情報がない場合においては T-Learner のパフォーマンスがよく、また、X-Learner は S-Learner のように CATE の推定値がゼロに寄るバイアスを有していないため、CATE が複雑な場合においても、実際の処置効果がゼロの場合の双方においても比較的よいパフォーマンスを出すとのことです。このあたりは、どういうケースを扱っているかを意識して Meta-Learner の選定を行う必要がありそうです。

#Domain Adaptation Learner のインスタンス作成
models = GradientBoostingRegressor(n_estimators=100, max_depth=6, min_samples_leaf=int(n/100), random_state=42)
final_models = GradientBoostingRegressor(n_estimators=100, max_depth=6, min_samples_leaf=int(n/100), random_state=42)
propensity_model = RandomForestClassifier(n_estimators=100, max_depth=6, min_samples_leaf=int(n/100), class_weight='balanced_subsample', random_state=42)
DA_learner = DomainAdaptationLearner(models=models, final_models=final_models, propensity_model=propensity_model)

#DA-Learner の訓練
DA_learner.fit(Y_train, W_train, X_train)

#テストデータでCATEを推定
DA_te = DA_learner.effect(X_test)

#CATEの推定結果を確認
print("CATE of DA-learner: ", round(np.mean(DA_te), 2))
> CATE of DA-learner: 809.83

print("Percentile of CATE of DA-learner: ", np.quantile(a=DA_te, q=[.05, .25, .5, .75, .95]))
> Percentile of CATE of DA-learner:  [-13049.88  -2217.02     14.32   3156.72  20295.17]

　
Domain Adaptation Learner は 3つのモデルを引数に取ります。Domain Adaptation Learner は $P(X^{0})$ と $P(X^{1})$ の確率分布が異なることを前提とした上で調整を行うため、事前に両者の確率分布の差異を確認しておくとよいのかもしれません。

それぞれテストデータで推定したCATEのばらつきをバイオリンプロットで確認します。

plt.violinplot([T_te, S_te, X_te, DA_te], showmeans=True)
plt.ylabel("Distribution of CATE")
plt.xticks([1,2,3,4], ['T-learner', 'S-learner', 'X-learner', 'DA-learner'])
plt.show()

おわりに

以上、『岩波データサイエンスvol.3』のCM接触の因果効果を Meta-Learner の各種手法を用いて推定してみました。今回は機械学習のモデルの調整が不十分だったり、cross validation を行っていなかったりとそもそもの予測精度の部分で十分じゃない部分が多いですが、まずは雰囲気をつかむことができればよいかなと思います。
特にどの Meta-Learner の手法を用いるべきかであったり、ベースモデルとして採用する機械学習モデルを何にするか、ハイパラチューニングをどう行うかといった点に関しては元論文も含めて十分に理解してから使うのがよさそうです。