はじめに
最近、データサイエンスの界隈でも因果推論に関する盛り上がりが以前にも増して見られるようになってきました。
本ブログでも過去に因果推論に関する記事を公開していますが、その中でも機械学習を活用した因果推論は最近のホットトピックの1つと言えます。
本記事ではもその盛り上がりに乗っかる形で、そのような機械学習を用いた因果推論の手法のひとつに挙げられる Causal Forest について、以前紹介した記事よりもより突っ込んで見ていきたいと思います。
内容としては R で提供されている grf パッケージの使い方についてより深く見ていきつつ、因果推論の界隈では有名な Lalonde のデータを用いて Causal Forest による平均因果効果 (ATE) の推定精度について検証をしていきます。
Lalonde データについて
まずは、本記事で扱う Lalonde のデータについて触れたいと思います。なお、Lalonde のデータについてすでに詳しい方は本節を読み飛ばしていただいてもかまいません。
Lalonde データとは
Lalonde のデータは Lalonde (1986) の中で*1、職業訓練プログラムの年収に対する効果をランダム化比較試験によって分析する際に用いられたデータです。Lalonde のデータは統計的因果推論の文脈で取り上げられることが多いのですが、その背景として、この実験から得られたデータと同様のメトリックを計測した他の職業訓練プログラムの観察データを組み合わせることで、これまでに様々な因果推論の推定精度の検証が行われてきたという経緯が存在します*2。通例、統計的因果推論を用いて因果効果を推定する際には正解となるデータがないのですが、この Lalonde はランダム化比較試験によって得られた結果という形である種の正解データが与えられているため、それが手法の精度を検証する際のベンチマークとして用いられるという訳です。
ちなみに、この Lalonde のデータのアウトカムは 1978年の年収で、共変量としては 1974年の年収 (一部欠損あり) と 1975年の年収、年齢、教育、人種、結婚の有無、学位の有無が存在します。
そのため、本記事でも同様のデータを用いて Causal Forest による因果効果の推定値とランダム化比較試験によって得られた結果を比べることで、Causal Forest による推定精度の検証を行うこととします。Causal Forest の新規性はどちらかとうと 条件付き平均因果効果 (CATE: Conditional Average Treatment Effect) の推定にあるのですが、Lalonde のデータからは CATE の推定ができないため、比較する対象は処置群 / 対処群の平均的な因果効果である 平均的因果効果 (ATE: Average Treatment Effect) とします。
Lalonde データとそれに結合するデータは R. Deheija 教授のページよりダウンロードできるため、こちらを使用することとします*3。Lalonde (1986) で用いられたデータである NSW データはランダム化比較試験によって得られた結果の確認のために用いるとともに、その対照群のデータを非実験データである PSID と CPS にそれぞれ結合することで、今回の検証に用いる非実験データを作成します。
# 各データのdtaファイルをインポート # NSW_DW は NSW データの中から 1974年の年収データが含まれるものだけを抽出したもの nsw_data <- read_dta("https://users.nber.org/~rdehejia/data/nsw.dta") nswdw_data <- read_dta("https://users.nber.org/~rdehejia/data/nsw_dw.dta") psid_data <- read_dta("https://users.nber.org/~rdehejia/data/psid_controls.dta") cps_data <- read_dta("https://users.nber.org/~rdehejia/data/cps_controls.dta") # データマージする際にエラーにならないよう仮の値で埋める (ただしこのカラムは使わない) nsw_data$re74 <- 0 # PSID / CPS のデータと NSW / NSW_DW データの処置群を結合 psid_nsw_data <- nsw_data %>% filter(treat==1) %>% rbind(psid_data) cps_nsw_data <- nsw_data %>% filter(treat==1) %>% rbind(cps_data) psid_nswdw_data <- nswdw_data %>% filter(treat==1) %>% rbind(psid_data) cps_nswdw_data <- nswdw_data %>% filter(treat==1) %>% rbind(cps_data)
これで、今回の検証で使用するデータを作成することができました。
ちなみに、各データセットの Treated / Control のデータ件数は下記の通りです。
| Dataset Name | Treated | Control | Data Type |
|---|---|---|---|
| NSW | 297 | 425 | Randomized Experiment |
| NSW-DW | 185 | 260 | Randomized Experiment |
| PSID NSW | 297 | 2,490 | Non-Experiment |
| CPS NSW | 297 | 15,992 | Non-Experiment |
| PSID NSW-DW | 185 | 2,490 | Non-Experiment |
| CPS NSW-DW | 185 | 15,992 | Non-Experiment |
ランダム化試験による因果効果
次に NSW / NSW-DW データにおける因果効果の計算結果を以下に記載します。前述の通り、これら両者はランダム化比較試験に基づくデータであるため、平均因果効果 ATE は単純に処置群 / 対照群それぞれの平均値を計算し、その差を取ることで得ることができます。すなわち、
であり、両データにおける値は以下の通りです。
| Dataset Name | tau |
|---|---|
| NSW | 886.3 |
| NSW-DW | 1,794.3 |
Causal Forest の推定結果の検証では、これらの値を比較対象 (Ground Truth) として用いることとします。
Causal Forest による因果効果の推定
次に、Causal Forest を用いて上述の PSID / CPS のデータでの平均因果効果の推定を行っていきます。使用するのは R の grf パッケージで、その中にある causal_forest() が Causal Forest のモデルを構築するための関数です。まずは、モデルに投入するデータの作成を行います。
# 特徴量X、アウトカムY、処置変数Wの行列 / ベクトルを作成 X_cpsdw <- cps_nswdw_data %>% dplyr::select(re74,re75,married,black,hispanic,education,age,nodegree) X_cpsdw <- X_cpsdw[1:16177,] Y_cpsdw <- cps_nswdw_data$re78[1:16177] W_cpsdw <- cps_nswdw_data$treat[1:16177]
次に、causal_forest() 関数を用いて Causal Forest のモデルを構築します。
causal_forest() 関数ではいくつかハイパーパラメータを設定する項目がありますが、まずはデフォルトパラメータでのモデル構築を行います。
# Causal Forest モデルの構築 tau_forest_cpsdw1 <- causal_forest(X_cpsdw, Y_cpsdw, W_cpsdw, seed=42)
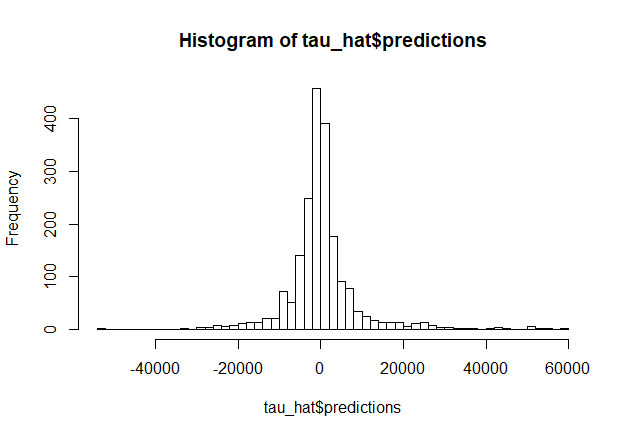
次に、上記モデルによる平均因果効果 ATE の推定結果を得ます。
OOB (Out-Of-Bag) 法による CATE の推定値は上記 Causal Forest オブジェクトの predictions パラメータで取得することができますが、これに二重にロバストな補正値を加えた推定結果を返す関数 average_treatment_effect() を使って ATE を計算した方がよりロバストな推定結果が得られるようです。average_treatment_effect() 関数はターゲットサンプル 4種 (all, treated, control, overlap) と二重にロバストな推定手法 2種 (AIPW, TMLE) を指定し ATE を算出することができますが、本記事ではターゲットサンプルに treated を、二重にロバストな推定方法に AIPW を設定して計算を行うこととします*4。
# AIPWを用いた二重にロバストな補正を加えた ATT の算出 att <- average_treatment_effect(tau_forest_cpsdw1, target.sample="treated", method="AIPW") print(paste("95% CI for the ATT:", round(att[1], 3), "+/-", round(qnorm(0.975) * att[2], 3)))
この関数を使って得られた ATE の推定結果を以下に整理しました。なお、上記のコードには載せていませんが、ターゲットサンプルと二重にロバストな推定方法を変えた場合の結果についても併せて記載します。
| Target Sample | Method | Estimate | 95% CI |
|---|---|---|---|
| all | AIPW | -2,440.277 | +/- 2,794.532 |
| all | TMLE | -3,003.918 | +/- 7,612.19 |
| treated | AIPW | 1,570.418 | +/- 1,343.229 |
| treated | TMLE | 2,040.887 | +/- 1,412.585 |
| control | AIPW | -2,491.009 | +/- 2,849.858 |
| control | TMLE | -3,050.461 | +/- 7,695.466 |
| overlap | AIPW | 1,100.529 | +/- 1,379.327 |
| overlap | TMLE | 1,100.529 | +/- 1,379.327 |
ターゲットサンプルを all と control に設定した場合の推定値が大きく乖離していますが、今回のケースにおいてはターゲットサンプルに all と control を指定した場合、処置変数Wの推定値が非常に小さい (<0.001) 場合が含まれており、関数の使用時にも警告メッセージが出力される形となっています。そのため、今回のケースでは treated ないしは overlap での推定値の算出が望ましいと言えます。
ちなみに推定精度に関してですが、NSW-DW データ単体で因果効果を算出した際の値が 1794.3 だったため、今回のケースで言うとターゲットサンプルに treated を設定した場合が比較的近しい値を導き出していると言えます。また、ターゲットサンプルに overlap を指定した場合はやや弱めの推定結果となっているようです。
複数データでの Causal Forest の検証
次に、前述の ATE の推定を他のデータセットでも行っていきます。ATE の推定に用いたコードは上述のものとほぼ同様なためここでは割愛をし、結果のみを記載する形とします。なお、NSW系のデータを用いる際は一部 1974年の年収データが欠損しているため、特徴量から 1974年の年収は除いてあります。
CPS NSW データ
| Target Sample | Method | Estimate | 95% CI |
|---|---|---|---|
| all | AIPW | -2,827.219 | +/- 3,249.853 |
| all | TMLE | -2,156.839 | +/- 8,143.334 |
| treated | AIPW | -314.239 | +/- 948.275 |
| treated | TMLE | 346.549 | +/- 1,057.594 |
| control | AIPW | -2,850.219 | +/- 3,363.521 |
| control | TMLE | -2,160.419 | +/- 8,272.053 |
| overlap | AIPW | -702.22 | +/- 1,018.522 |
| overlap | TMLE | -702.22 | +/- 1,018.522 |
PSID NSW-DW データ
| Target Sample | Method | Estimate | 95% CI |
|---|---|---|---|
| all | AIPW | -3074.639 | +/- 7,142.742.532 |
| all | TMLE | -2,701.204 | +/- 17,053.764 |
| treated | AIPW | 1,346.644 | +/- 1,464.634 |
| treated | TMLE | 1,947.960 | +/- 2,689.818 |
| control | AIPW | -3335.734 | +/- 8.265.459 |
| control | TMLE | -2,948.971 | +/- 18,476.725 |
| overlap | AIPW | -973.849 | +/- 1855,922 |
| overlap | TMLE | -973.849 | +/- 1855,922 |
PSID NSW データ
| Target Sample | Method | Estimate | 95% CI |
|---|---|---|---|
| all | AIPW | -6,069.643 | +/- 3,733.312 |
| all | TMLE | -7,546.493 | +/- 10,493.081 |
| treated | AIPW | -1,818.175 | +/- 1,685.093 |
| treated | TMLE | 644.434 | +/- 2,886.789 |
| control | AIPW | -6,621.029 | +/- 4,578.663 |
| control | TMLE | -8,024.739 | +/- 11,999.54 |
| overlap | AIPW | -3,475.897 | +/- 1,696.031 |
| overlap | TMLE | -3,475.897 | +/- 1,696.031 |
結果として、PSID NSW-DW データでの treated の推定値が比較的ましといった程度で、CPS NSW や PSID NSW データではランダム化比較試験で得られた結果からいずれもかなり程遠い結果となってしまいました。このままでは到底結果の信頼性が欠けるため、何かしらの形で推定結果を改善するためのアクションが必要と言えます。
ここから先は、モデルの推定結果を向上させるための特徴量選択やハイパーパラメータチューニングについて試していく必要がありそうですが、いったん文字数が多くなってしまったため本記事はいったんここで区切り、次回別の記事で左記の特徴量選択やハイパーパラメータチューニングについて試していければと思います。
統計的因果推論の関連記事
*1:https://www.jstor.org/stable/1806062?seq=1
*2:一例としてはhttps://amstat.tandfonline.com/doi/abs/10.1080/01621459.1999.10473858#.XmI97Kj7Q2w
*3:https://users.nber.org/~rdehejia/
*4:ちなみにこの average_treatment_effect() 関数はサブセットとして特徴量Xの条件を指定することで CATE の推定も可能になっています。